L-system generator
(→Additional notes) |
(→Examples) |
||
| Line 96: | Line 96: | ||
== Examples == | == Examples == | ||
| − | Next table illustrates the interpretation of L-system generated strings. Left column presents L-system generated string and right column graph that is created when string is parsed. In this example we are interested in actual L-systems that generate left column strings. Notice that different strings may generate identical graph. Graph circles represent topics. Number (or letter) in circle is topic's identity. Lines between circles represent associations. | + | Next table illustrates the interpretation of L-system generated strings. Left column presents L-system generated string and right column graph that is created when string is parsed. In this example we are not interested in actual L-systems that generate left column strings. Notice that different strings may generate identical graph. Graph circles represent topics. Number (or letter) in circle is topic's identity. Lines between circles represent associations. |
{| border="1" cellpadding="4" | {| border="1" cellpadding="4" | ||
Revision as of 12:40, 18 December 2008
Wandora's L-system generator is used to construct topic map graphs using formal grammar called L-systems. L-systems are generally known as iterative computational methods used to generate self-similar fractals, usually plants and other biological organisms.
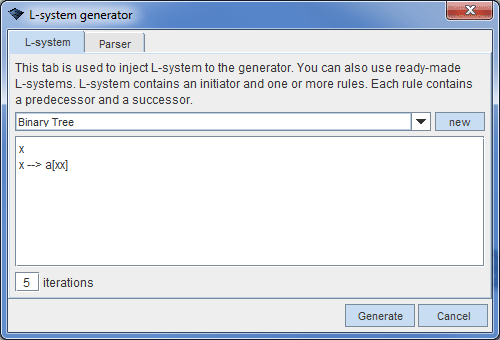
Wandora's L-system generator starts with File > Generate > L-system generator.... Option opens a dialog with two tabs: L-system and Parser. By default the L-system tab is active. L-system tab is used to enter actual L-system to the generator. Below is a snapshot of L-system tab view in Wandora. Tab contains also drop-down-selector to select ready-made L-systems. User can also store his/her own L-system by clicking new button and entering name for the L-system into a dialog Wandora opens. Wandora stores L-systems to options.
L-system contains in Wandora
- An initiator
- One or more rules
Initiator is the first line in L-system. It is usually an alphabet or set of alphabets. Initiator initializes the L-system string. For example, the snapshot above has an L-system with initiator x.
L-system rules have always two parts: Predecessor and successor. Rule is executed whenever L-system generated string contains predecessor. Predecessor is replaced by successor string during the rule execution. For example, the snapshot L-system above contains one rule where predecessor is x and successor is a[xx]. Wandora assumes predesessor and successor are separated with -->.
L-system execution continues only limited time. Each execution step is called iteration. Text field below the L-system definition text area contains number of L-system iterations. As L-system string may grow exponentially large it is suggested you not to use more than 10 iterations unless you are sure about the outcome of L-system.
As iteration continues the initiator string is gradually changed by rules. For example examining the snapshot above initiator x is changed:
0: x 1: a[xx] 2: a[a[xx]a[xx]] 3: a[a[a[xx]a[xx]]a[a[xx]a[xx]]] 4: a[a[a[a[xx]a[xx]]a[a[xx]a[xx]]]a[a[a[xx]a[xx]]a[a[xx]a[xx]]]] etc.
As you notice, the string grows very rapidly.
L-systems itself carry no interpretation of generated string. Generated strings are semantic free, you could say. This reflects to Wandora's L-system generator feature also. L-system string generation is separated from the interpretation. Interpretation is handled by special L-system string parser that reads the generated string and interprets each token in the string. You can also use the parser independently of L-system string generation. Independent usage of parser happens in Parser tab.
L-system string interpretation
Typically L-system string is interpreted to turtle commands such as move forward, draw line, and turn left or right. However, such interpretation has implicit assumption of external environment where you can express ideas of left and right direction for example. If you consider plain graphs, there is no such external world we could refer. Turtle command "turn left" has no meaning in plain graph mode as we have no external coordinate system outside the graph. Thus Wandora interprets L-system string little different compared to usual L-systems. The vocabulary and it's interpretation are explained in the table below.
General principle is that each alphabet in vocabulary creates a topic i.e. a node of the graph and associates it with some other topics, usually at least the previously created topic. Association is a graph edge in the topic map world. When topic (excluding named topics) is created, global variable called topic counter is increased by one. When L-system string parsing starts, topic counter is 0. Topic counter is used to derive topic's identity. Thus, topic is merged with existing topic with same topic counter.
Different parenthesis are used to control branching of the graph. Branching means that at least first topic in the branch is associated to the "body". Branch typically ends (closes) somewhere in the string and graph generation returns to the "body".
Capital alphabets are used to create named topics. Named topic has strong identity. This means that named topic is always same. Named topics allow you to refer same topic everywhere in the L-system string.
Coloring of associations and topics refers association and topic typing. When we say topic is colored by e then topic is typed by topic derived from alphabet e. Same applies to associations. When association is colored by e then association type topic is derived from alphabet e.
| Alphabet(s) | Interpretation |
| a | Creates a topic and associates it with previously created topic. If no previous topic exists, no association is created. |
| A-V | Create named topic and associate it with previously created topic. Named topic merges with previously created topic with same name. Unfortunately vocabulary supports only 23 different named topics. |
| eiouy | Create a colored topic and associate it with previously created topic using colored association. Colored topic means here that topic is typed. Colored association means here that the association type is different. Notice the set is equal to vowel characters (a taken out). |
| : followed with any of a-zA-Z1-9 | Change global color i.e. topics and associations are colored after this point. |
| :0 | Reset global color. |
| ( | Start sequential block. First topic in the sequential block is associated with the topic before the block. Topic's created after sequential block has been closed are associated to topics created before the block. Blocks are used to branch graph. |
| ) | Close sequential block. |
| [ | Start parallel block. All topics in the parallel block are associated with the topic before the block. |
| ] | Close parallel block. |
| { | Start cyclic block. First topic in the sequential block is associated with the topic before the block. Last topic in the cycle block is associated with first topic in block. |
| } | Close cyclic block. |
| - | Subtract topic counter by one. The effect is that next topic is merged with previous topic. |
| + | Add topic counter by one. The effect is that there is a gap in topic numbering. |
| 0 | Reset topic counter. |
Other alphabets have no explicit semantic and are silently passed by parser. Other alphabets, such as x and z are usually used as L-system rule predecessors. However, notice the y alphabet is reserved for colored topic creation.
Examples
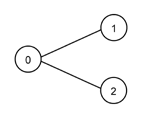
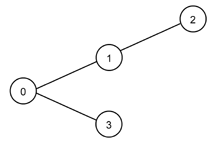
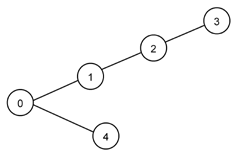
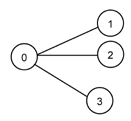
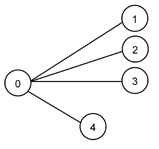
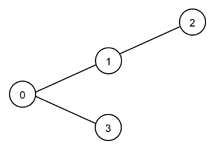
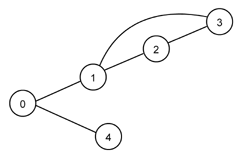
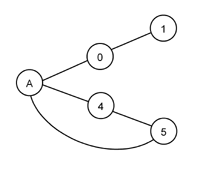
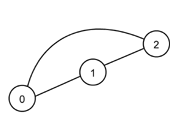
Next table illustrates the interpretation of L-system generated strings. Left column presents L-system generated string and right column graph that is created when string is parsed. In this example we are not interested in actual L-systems that generate left column strings. Notice that different strings may generate identical graph. Graph circles represent topics. Number (or letter) in circle is topic's identity. Lines between circles represent associations.
| Parsed String | Generated Graph |
|
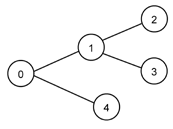
aa or a(a) or a[a] or a{a} |
|
|
aaa or a(aa) or a(a(a)) |
|
|
a(a)a or a[a]a or a{a}a |
|
|
a(aa)a or a(a(a))a |
|
|
a(aaa)a or a(a(aa))a or a(a(a(a)))a |
|
|
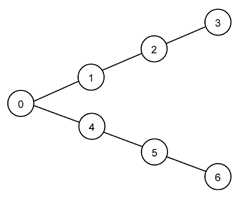
a[aa]a |
|
|
a[aaa]a |
|
|
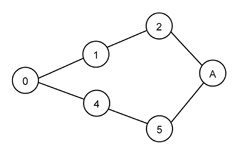
a{aa}a |
|
|
a{aaa}a |
|
|
a{aaaa}a |
|
|
a(a(a)a)a or a(a[aa])a |
|
|
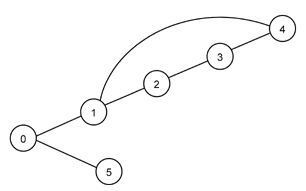
a(aaa)aaa |
|
|
a(aaA)aaA |
|
|
A(aa++)aaA |
|
|
aaa---a |
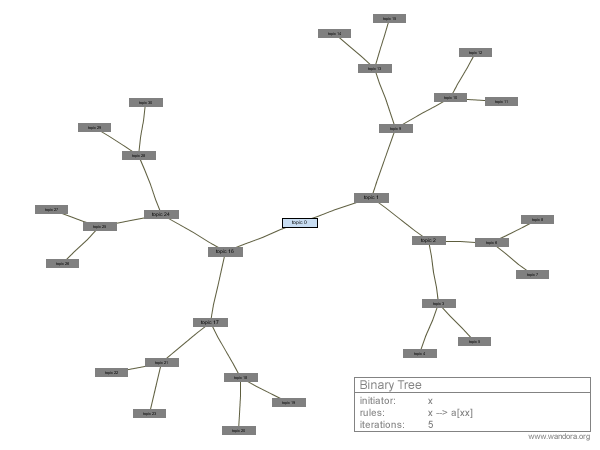
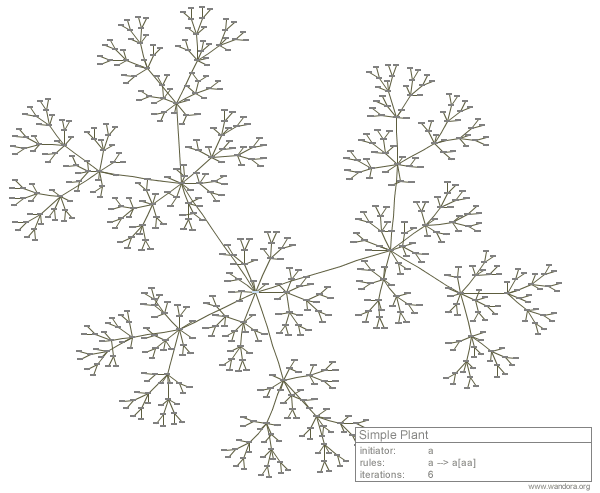
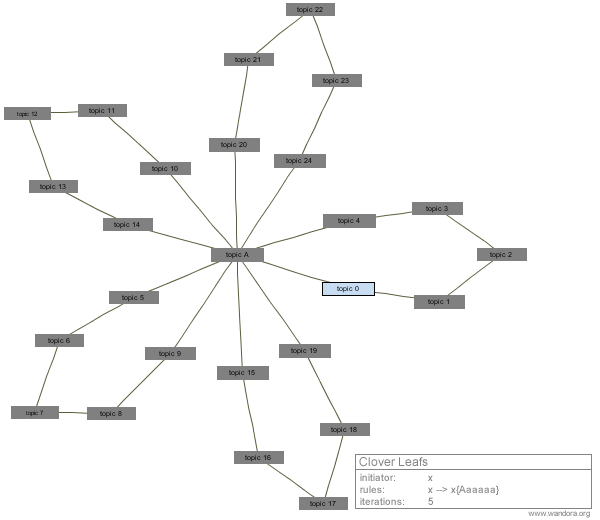
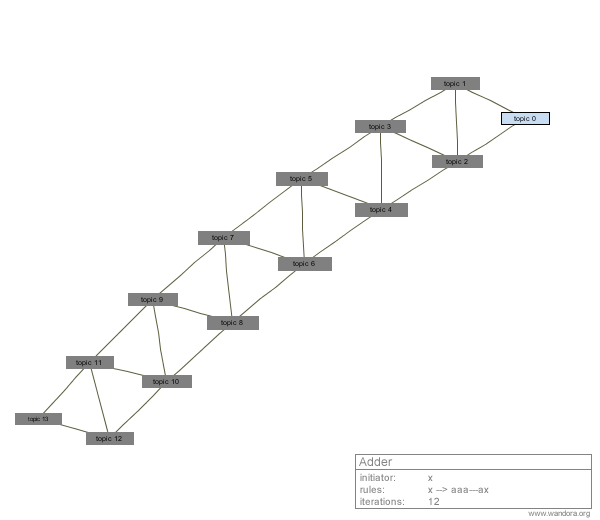
Next images illustrate actual L-systems and equivalent topic map graphs visualized in Wandora. Grey boxes represent topics and lines associations between topics. A table expressing L-system initiator, rules, and number of iterations is next to the graph.
Additional notes
- The L-system vocabulary interpretation was an ad hoc invention. It is likely that current vocabulary interpretation doesn't cover all possible topic maps. In other words there are topic maps that can not be generated with current L-system interpretation. Wandora Team welcomes all criticism, feedback, and ideas. Evident limitations are
- The L-system interpretation allows only binary associations. You can't generate associations with three players for example.
- The L-system interpretation supports only 23 [A-V] different "static" topics.
- L-system generator creates numbered topics and numbering starts always from 0. Thus, generating two L-systems consequently generates same topics and associations created during first round remain. This feature may confuse user if he/she tries L-system generator many times consequently without resetting Wandora's topic maps. To avoid L-system interference user has to initialize Wandora between L-system generations with File > New Project option.
- User should not see this as a bug but a feature as it allows user to apply several different L-systems consequently to one topic map.
- It was expressed above that used interpretation of L-system does not use any external coordinate system to place nodes and edges of the generated graph. Now, watching nicely rendered graph examples above may suggest something very different. Example graphs looks carefully rendered. However, the carefully rendered look was achieved using Wandora's Graph topic panel. Panel has it's own mechanism to unwrap and clear up complex graphs. Although mechanism results topologically similar graphs, it is very likely that user trying out example L-systems perceives small variations in his/her renderings.