Finite group graph generator
From WandoraWiki
(Difference between revisions)
| (2 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
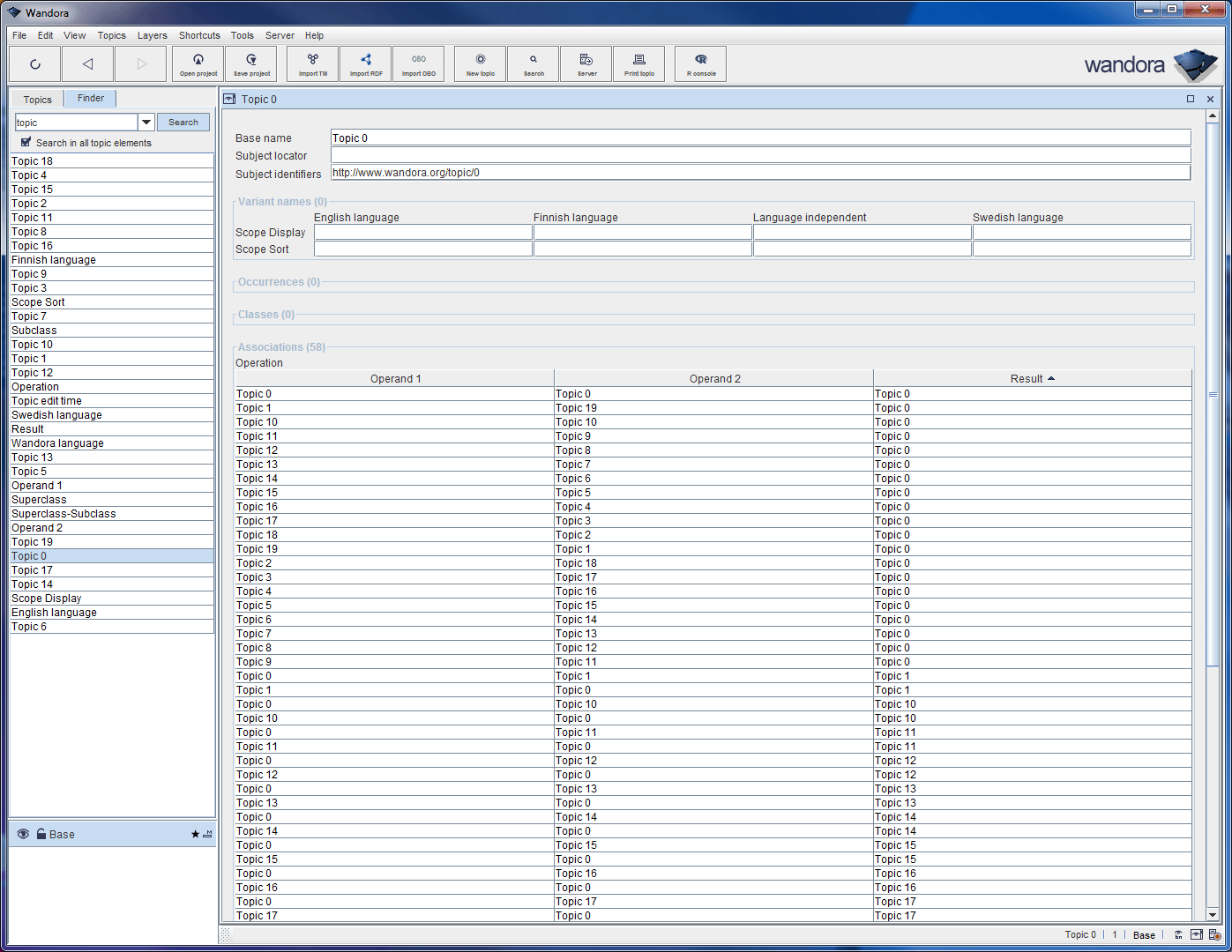
| − | Finite group graph generator creates a cyclic group with prime order given by the Wandora user. Below is a graph visualization of finite group with a prime order 20 and it's '''Topic 0''' element. Visualization contains only association of '''Topic 0''' node. All associations are triplets of two operands and a result. | + | Finite group graph generator creates a cyclic group with a prime order given by the Wandora user. Below is a graph visualization of finite group with a prime order 20 and it's '''Topic 0''' element. Visualization contains only association of '''Topic 0''' node. All associations are triplets of two operands and a result. |
[[Image:finite_group_example.gif|center]] | [[Image:finite_group_example.gif|center]] | ||
| − | Looking at '''Topic 0''''s association reveals the nature of associations. Each association represents an operation with two operand topics and a result topic and result is a "sum" of operands. For example operands '''Topic 2''' and '''Topic 4''' form an association with a result '''Topic 6''' because '''2 + 4''' is equal to '''6'''. | + | Looking at '''Topic 0''''s association reveals the nature of associations. Each association represents an operation with two operand topics and a result topic and result is a "sum" of operands. For example, operands '''Topic 2''' and '''Topic 4''' form an association with a result '''Topic 6''' because '''(2 + 4) mod 20''' is equal to '''6'''. Operands '''Topic 1''' and '''Topic 19''' form an association with a result '''Topic 0''' because '''(19 + 1) mod 20''' is equal to '''0'''. |
| + | |||
[[Image:finite_group_example2.gif|center]] | [[Image:finite_group_example2.gif|center]] | ||
| + | |||
== See also == | == See also == | ||
Latest revision as of 13:37, 22 February 2013
Finite group graph generator creates a cyclic group with a prime order given by the Wandora user. Below is a graph visualization of finite group with a prime order 20 and it's Topic 0 element. Visualization contains only association of Topic 0 node. All associations are triplets of two operands and a result.
Looking at Topic 0's association reveals the nature of associations. Each association represents an operation with two operand topics and a result topic and result is a "sum" of operands. For example, operands Topic 2 and Topic 4 form an association with a result Topic 6 because (2 + 4) mod 20 is equal to 6. Operands Topic 1 and Topic 19 form an association with a result Topic 0 because (19 + 1) mod 20 is equal to 0.