Finite group graph generator
From WandoraWiki
(Difference between revisions)
| Line 4: | Line 4: | ||
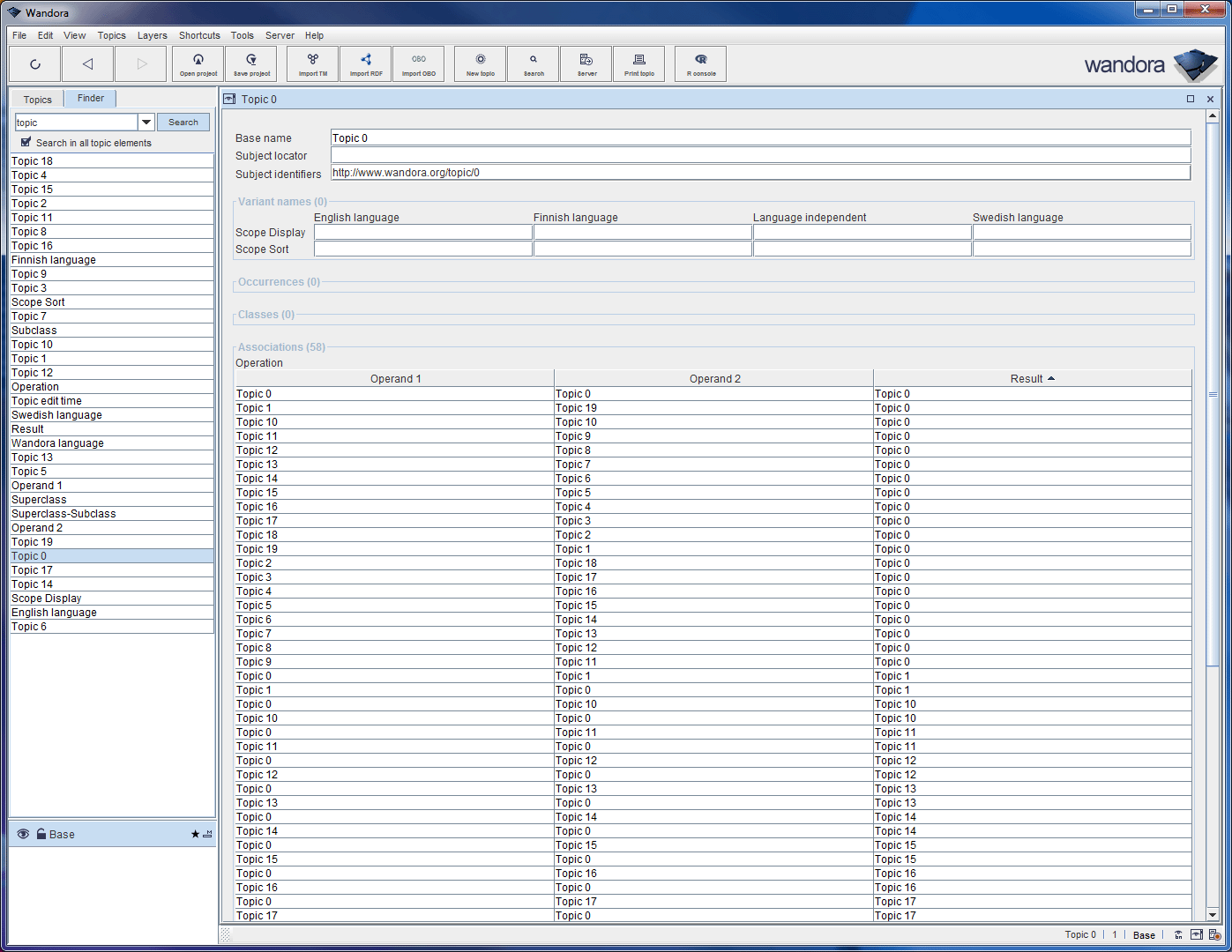
Looking at '''Topic 0''''s association reveals the nature of associations. Each association represents an operation with two operand topics and a result topic and result is a "sum" of operands. For example operands '''Topic 2''' and '''Topic 4''' form an association with a result '''Topic 6''' because '''2 + 4''' is equal to '''6'''. | Looking at '''Topic 0''''s association reveals the nature of associations. Each association represents an operation with two operand topics and a result topic and result is a "sum" of operands. For example operands '''Topic 2''' and '''Topic 4''' form an association with a result '''Topic 6''' because '''2 + 4''' is equal to '''6'''. | ||
| + | |||
[[Image:finite_group_example2.gif|center]] | [[Image:finite_group_example2.gif|center]] | ||
| + | |||
== See also == | == See also == | ||
Revision as of 13:35, 22 February 2013
Finite group graph generator creates a cyclic group with a prime order given by the Wandora user. Below is a graph visualization of finite group with a prime order 20 and it's Topic 0 element. Visualization contains only association of Topic 0 node. All associations are triplets of two operands and a result.
Looking at Topic 0's association reveals the nature of associations. Each association represents an operation with two operand topics and a result topic and result is a "sum" of operands. For example operands Topic 2 and Topic 4 form an association with a result Topic 6 because 2 + 4 is equal to 6.